ASPEN 学习笔记 21： 精馏回顾

ASPEN 学习笔记 21： 精馏回顾

ASPEN 学习笔记 21： 精馏回顾

基本概念

  • 纯物质蒸气压 vapor pressure

    • 对于纯物质，其相态之间平衡，气相压力为其饱和蒸气压，而饱和蒸气压仅仅与温度有关
    • 比如在计算温湿度时要计算水的饱和蒸气压，可以引用wexler公式，

          \[P^S = f(T)\]

      具体的表达方式可以参考相关文献，这里了解此概念即可。

  • 二元Txy 和 xy 相图

    • 在一定压力的前提下，二元混合物的Txy相图类似如下，x为液相组成，y为气相组成；后续精馏分析时会用到
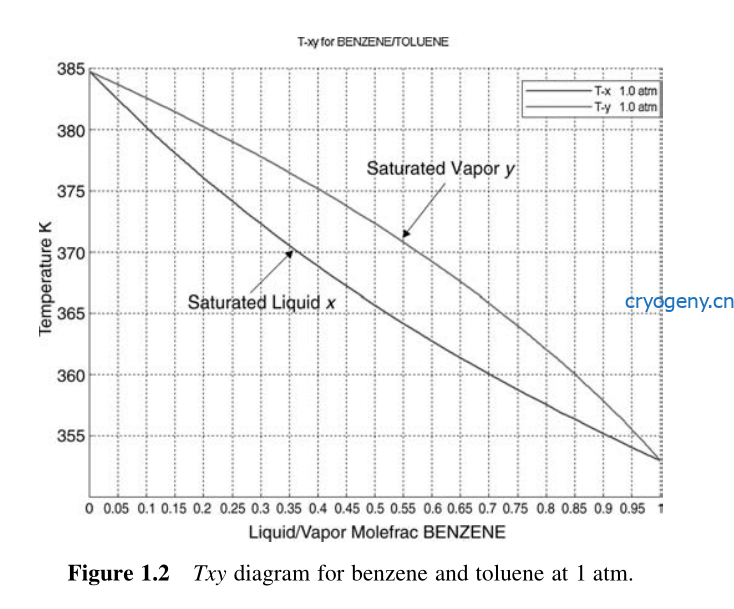
    • image
    • xy 如下图
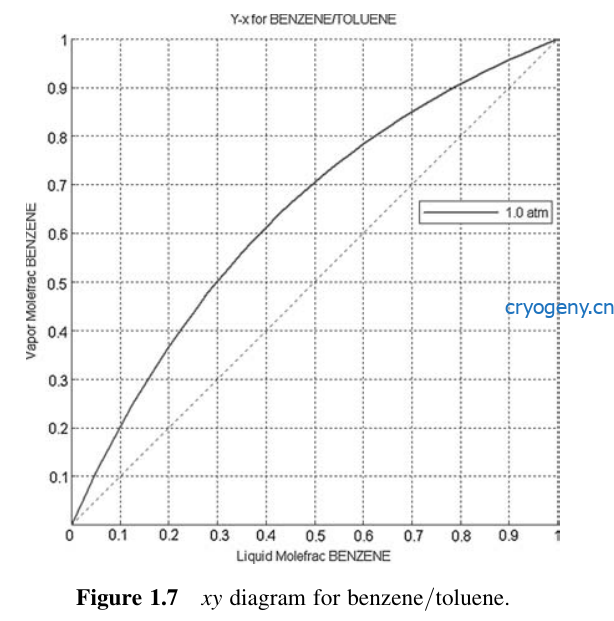
    • image

  • 物性计算--参考本系列文章的物性计算选择路线

  • 相对挥发度 relative volatility

    • 对于二元系统，定义相对挥发度为

          \[\alpha_{LH}= \frac{y_L/x_L}{y_H/x_H}\]

    • 由于是二元系统，气相组分分数相加为1，而液相组分分数相加也为1 从而得到

          \[y= \frac{\alpha x}{1+ (\alpha -1 )x}\]

    • 对于多元系统（N组分），定义最重的组分为H，而任意组分为j ，则任意组分相对H的挥发度为

          \[\alpha_j =\frac{y_i/x_i}{y_H/x<em>H}\]

      同样的，由于所有气相组分分数之和为1，即

          \[\sum^N</em>{j=1} y_i =1\]

    • 可以求得

          \[\sum ^N _{j=1 } y<em>i =1 = \sum ^N </em>{j=1} \alpha _j x_j \frac{y_H}{x_H} = \frac{y_H}{x<em>H}\sum^N</em>{j=1}\]

    • 最终有

          \[\frac{y_H}{x<em>H} = \frac{1}{\sum^N</em>{j=1} \alpha_j x_j}\]

      以及

          \[y_i = \frac{\alpha _j x_j}{\sum ^N _j \alpha_j x_j}\]

    • 同样也可以得到x的表达式

  • 泡点计算 bubble point calculation，也是相平衡的计算

    • 化学势能 chemical potential 在相平衡时，气相化学势能和液相化学势能相等，即

    •     \[\mu ^L _j = \mu ^V _j\]

    • 对于液相，引入活度系数和饱和蒸气压，对于气相，引入逸度系数和总压力，则上式更新如下

    •     \[x_j P^S_j \gamma _j = y_j P \delta _j\]

    • 假设液相溶液比较理想，则可认为活度系数为1，总压力不太高的情况，可以认为逸度为1，由于气相中各组分分数的和为1，得到以下

    •     \[P = \sum ^N _{j=1} x_i P ^S _j\]

  • 非理想的VLE

    • 上面的假设活度系数和逸度均为1，实际上只有在所有的组分都比较相似的情况下成立，一般都会有偏差，这时就会有非理想的VLE 气液平衡。
    • 共沸： 气相和液相中的组成相同，此时精馏不能再进行，某些时候，共沸也视作 精馏边界
    • 在aspen中，可以直接使用菜单栏中 共沸搜索， zeotropic search，其会对组分进行自动的共沸分析。可以采用split 或者 distil 模块

Tags: , , , , , ,

发表回复